Effetto tunnel quantistico
Avete mai sentito parlare di effetto tunnel? No? Allora considerate cosa succede ad un ciclista se la rincorsa che prende per superare una collinetta non è sufficiente? Poiché la sua energia è inferiore di quella che servirebbe per oltrepassare il dosso, la bicicletta si fermerà ed il povero ciclista dovrà ritornare indietro.
Questo è quello che avviene se consideriamo la meccanica classica, ma quando abbiamo a che fare con le particelle, e quindi con la meccanica quantistica, i comportamenti diventano più bizzarri.
Una particella è descritta da una funzione d’onda e questo vuol dire che nello spazio essa assumerà tutte le possibili posizioni ma con diversa probabilità. Detto in termini semplici, se un’onda si propaga verso una barriera, dopo un certo tempo la funzione d’onda sarà diversa da zero sia prima che dopo la barriera. Vuol dire che non sempre l’onda sarà respinta dalla barriera, in alcuni casi essa potrà oltrepassarla.
Quello che potrebbe apparire una contraddizione, si chiama “effetto tunnel” ed è alla base del funzionamento di molti dei dispositivi con cui abbiamo a che fare ogni giorno, per la maggior parte composti da circuiti integrati fatti di Transitors che sfruttano proprio questa proprietà dei semiconduttori.
Potete provare dal vivo l’effetto tunnel giocando con l’applicazione messa a disposizione dall’Università del Colorado. L’esperimento consiste nel lanciare contro una barriera una particella ed osservare il comportamento della sua funzione d’onda variando le caratteristiche sia dell’onda che della barriera.
Come si conduce l’esperimento effetto tunnel quantistico?
La prima cosa da scegliere è la tipologia di barriera di energia potenziale che può essere singola o doppia.
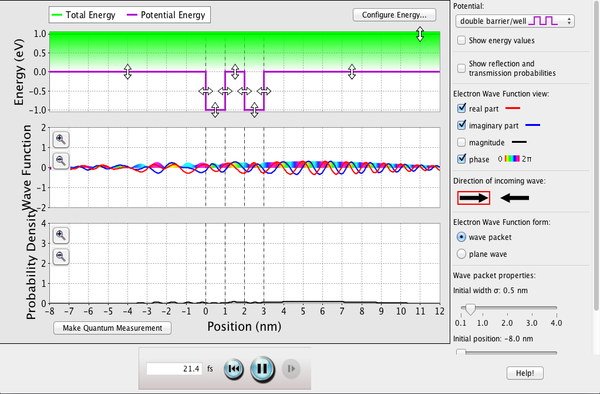
Nei tre grafici potrete osservare:
- Energia eV: le due energie in gioco, quella della particella e della barriera energetica ed è possibile cambiarle trascinando le frecce con il mouse
- Funzione d’onda: la funzione d’onda
- Densità di probabilità: la probabilità di osservare la particella prima e dopo la barriera.
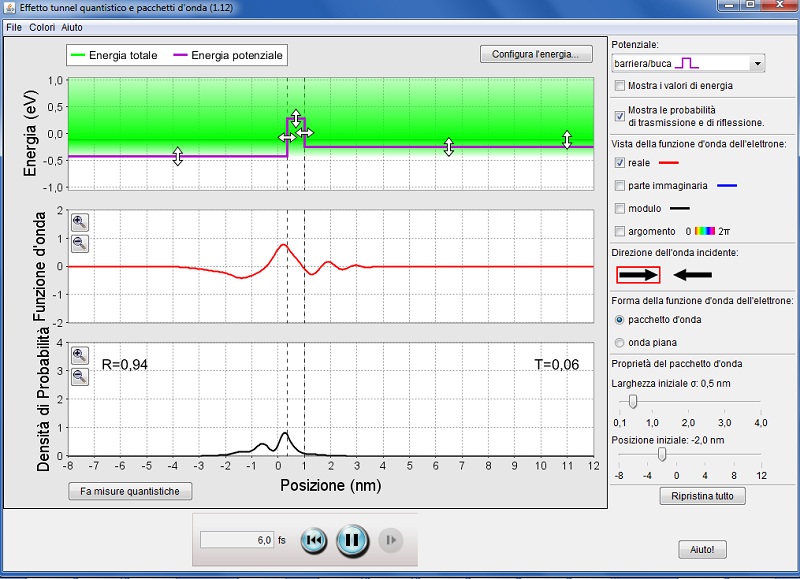
Provate a variare la barriera energetica sia in ampiezza che in altezza per verificare i diversi comportamenti della funzione d’onda. Scoprirete che l’onda non scompare del tutto al di là della barriera: una parte verrà respinta ma un’altra parte riuscirà ad oltrepassarla e questo, ovviamente, avviene con probabilità diverse a seconda dell’energia.
Nella figura, ad esempio, le condizioni impostate per l’energia consentono il passaggio del 6% delle particelle nonostante non posseggano l’energia sufficiente ad oltrepassare la barriera.
L’applicazione è realizzata in Java: cliccando sull’immagine potrete sia scaricarla sul vostro computer per giocarci offline che eseguirla direttamente se nel vostro browser è abilitata l’esecuzione delle applet Java.
Quasi dimenticavo: non si tratta di magia o di fantasia. E’ tutto rigorosamente vero e basato sull’equazione di Schrődinger che descrive l’evoluzione del tempo del modulo quadro della funzione d’onda che corrisponde alla probabilità di osservare una particella in una data posizione.